CGeNArateWeb Help - Method
Method Help
In the CGeNArate model, DNA is represented in Cartesian 3D space, using one bead per nucleotide located at the C1' atom of the sugar. The Energy of the interactions between the particles are divided between remote non-bonded terms (LJ and Debye-Hückel), and sequence-dependent interactions represented by truncated polynomial expansions $$E = \sum_{a=2}^4 K_a(l-l_0)^a, \sum_{a=2}^4 K_a(\alpha-\alpha _0)^a,$$ following Savelyev and Papoian's fan interaction model (Proc. Natl. Acad. Sci., 2010):
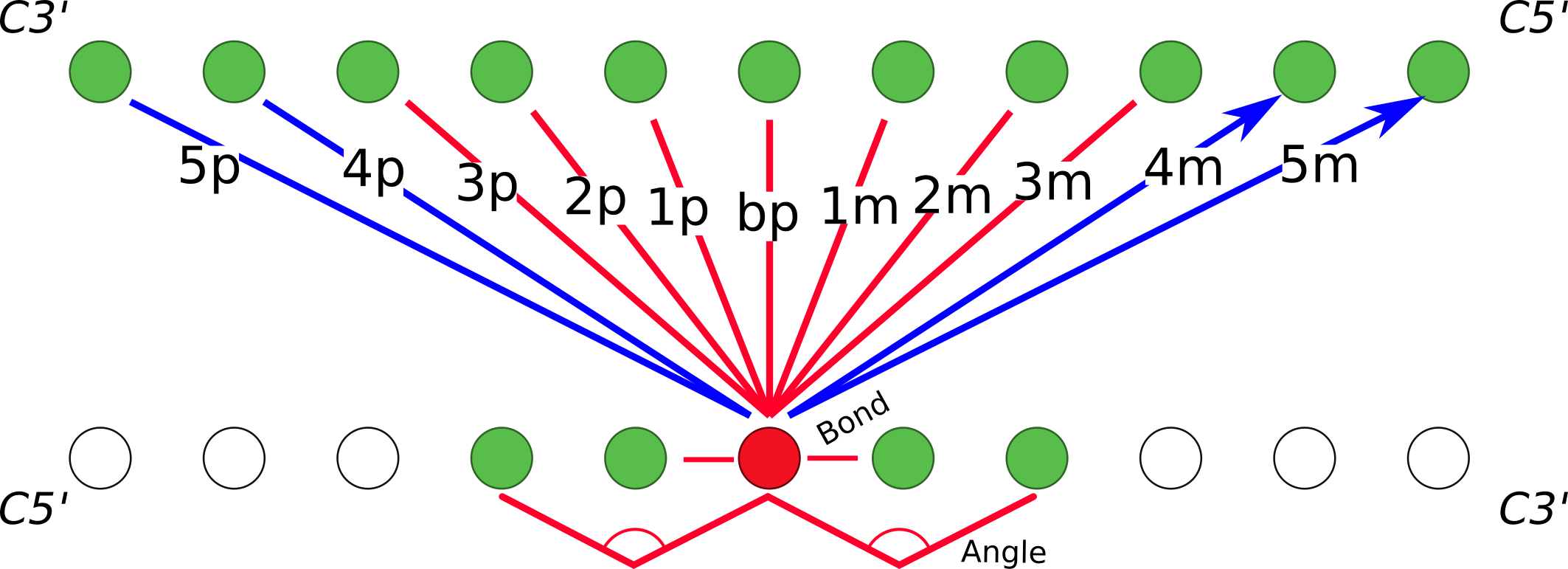
The parameters of the generalized harmonic potentials (interaction coefficients and reference equilibrium values) for each interactions are derived from the miniabc set (a minimal set of sequences (13 sequences of 18 bp) in which all 136 unique tetranucleotide combinations appear) of atomistic molecular dynamics simulations simulated with the parmbsc1 force field (Dans et al., Nucleic Acid Res, 2019).
CGeNArateWeb
CGeNArateWeb runs a Langevin Dynamics simulation for a given sequence of DNA. It integrates the equations of Motion at a given Temperature using the Velocity Verlet algorithm with an integration step of 0.1ps, and produces a Coarse Grained Molecular Dynamics simulation.
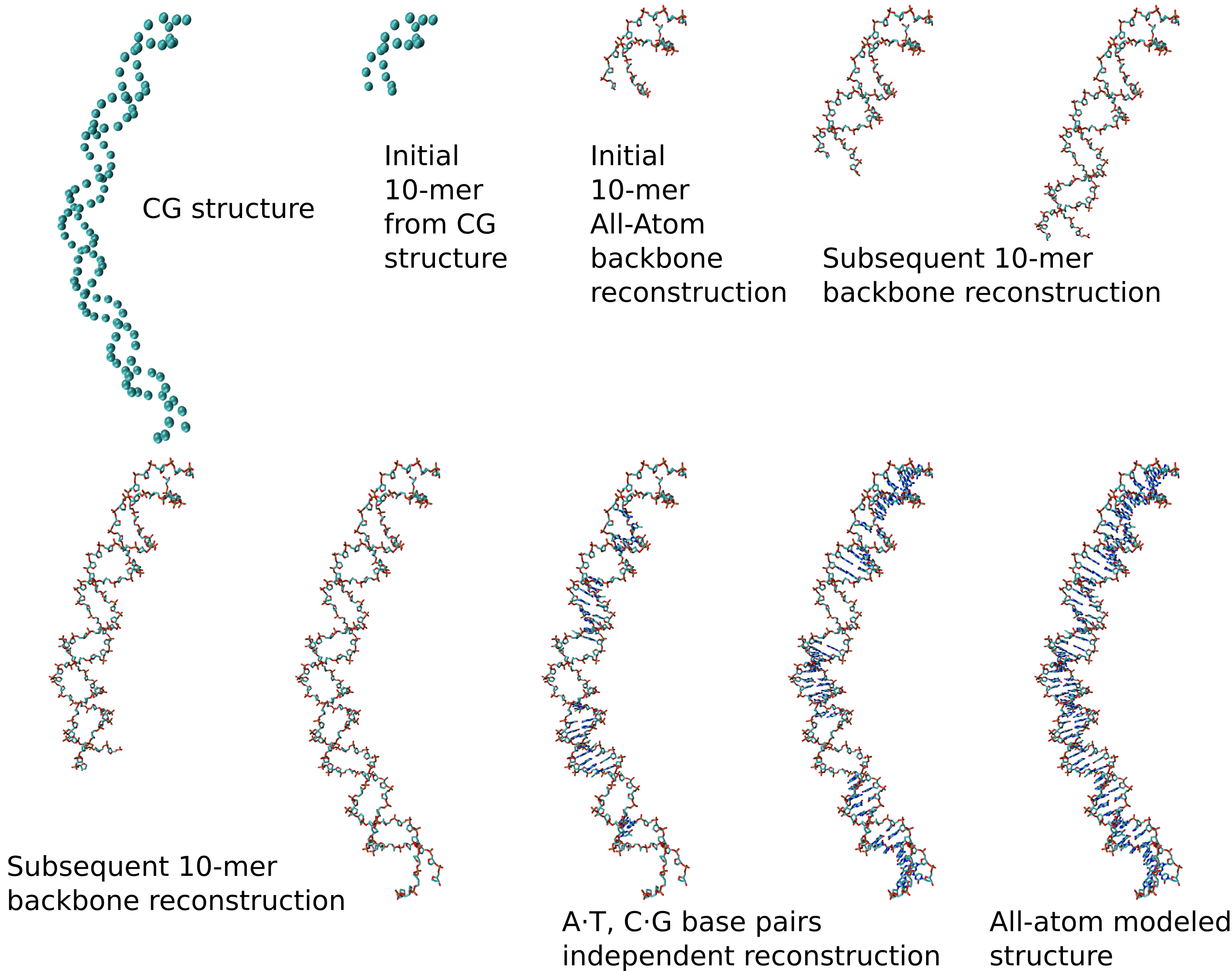
After the simulation, we use the GLIMPS model (Louison et al., J. Chem. Theory Comput., 2021) to rebuild the backbone of the DNA using the backbone positions, iteratively for each 10-mer. Then, a base-pair dependent GLIMPS model rebuilds the corresponding bases in the space created by the backbone.
Circular CGeNArate
The algorithm for circular DNA maintains the ends of the DNA attached, analogously to the rest of the B-DNA (for theoretical background about circular DNA check the last paragraph of this secion). In the simulation of circular DNA the starting structure is a plane circle with a given linking number $\Delta Lk$. To construct the circular starting structure two steps are needed. First the linear starting structure is constructed with fdhelix, by David A. Case., and then the linear structure is deformed to create a the planar circle with the desired Linking Number are built using a Python script.

Theoretical background of circular DNA: An important feature of a circle is that the linking number is constant. Twist $Tw$ reflects the number of helical turns and writhe $Wr$ is the number of times the double helix crosses over on itself (supercoils). The relaxed structure for the circle is defined as the structure with $Wr = 0$ and twist values are the values of the relaxed twist state. Thus the total linking number $Lk_0$ of the relaxed circle is $Lk_0 = Tw_0$. To induce additional stress the twist value of each base pair step of the circle can be changed, which results in new value of $Tw$. Over- or under-twisting of the relaxed structure results in a different linking number $\Delta Lk = Lk - Lk_0 = Tw - Tw_0$, and thus a different starting structure with $\Delta Lk \neq 0$. $\Delta Lk$ can only take integer values, corresponding to the amount of initial helical turns. $\Delta Lk = Tw + Wr$ will stay constant throughout the whole simulation, however $Tw$ will change throughout the simulation and $Wr$ becomes non-zero. The value of $\Delta Lk$ can be chosen in the Input parameters.
CGeNArate + Proteins
The algorithm of 'CGeNArate + Proteins' works the same way as the unconstrained CGeNArate with Langevin Dynamics, where the Energy is given by sequence-dependent polynomial interactions. However, the DNA which is bound to the protein is constrained. The base-pairs bound to the protein are kept rigid with the reference values (distances and angles), extracted from the X-ray crystal structure of the protein-DNA complex in the PDB. In the 'Input' section you can choose the protein of interest from an extensive list of protein-DNA complexes. For example the protein-DNA complex 1a0a is bound to 16 base pairs of DNA. If you choose in the 'Input' initial position 3, the base pairs 3 to 18 are kept rigid according to reference values of the DNA in the 1a0a complex. The sequence the user inputs for the bound DNA does not matter in this case.
Note: The protein itself does not directly contribute to the simulation (apart from the conformation imposed on the protein-bound DNA, and a nonbonded interaction to avoid overlaps), and the 3D output of the trajectory the protein structure of the protein-DNA complex is superimposed onto the DNA for visualization and analysis purposes.
