MC DNA Help - Analysis Bending
Bending
- Method
- Table of values for bending of the whole DNA fiber
- Bending distribution of 5/10 bp segments
- Bending distribution of 5/10 bp segments and the whole fiber
- Bending of 5/10 bp segments in xz/yz direction along sequence
- Distribution of contributions of xz- and yz-bending to total bending of whole fiber
- Bending of whole fiber along trajectory
Method
The bending of the DNA fiber is calculated based on the values of the rotational base-pair step parameters tilt, roll and twist. The total bending angle of a segment of k base-pairs of DNA of N base-pairs starting at base-pair n is calculated according to
$$B_n^{tot}(k) = \sqrt{b_n^x(k)^2 + b_n^y(k)^2}$$
`b_n^x(k)` and `b_n^y(k)` are the bending contributions in xz- and yz- plane of a segment of k base-pairs. The directions of the x,y and z-axis here determined by the first base-pair. The definition of the directions of the axes x,y and z is given in “Methods”. `b_n^x(k)` and `b_n^y(k)` are calculated according to Equation (7) and (8) of Battistini et al., J Mol Bio (2010):
\[b_n^x(k) = \sum_{i=n}^{k + n - 1} \rho_i cos \Phi_i + \sum_{i=n}^{k + n - 1} \tau_i sin \Phi_i \]
\[b_n^y(k) = \sum_{i=n}^{k + n - 1} \rho_i sin \Phi_i + \sum_{i=n}^{k + n - 1} \tau_i cos \Phi_i \]
k in the analysis is chosen to be half-turn (5bp), full turn (10bp) and the length of the whole fiber N. `\tau_i` `\rho_i` and `\Phi_i` are the values of tilt, roll and cumulative twist of base-pair step i.
Table of values for bending of the whole DNA fiber (available for Structure Flexibility Analysis)
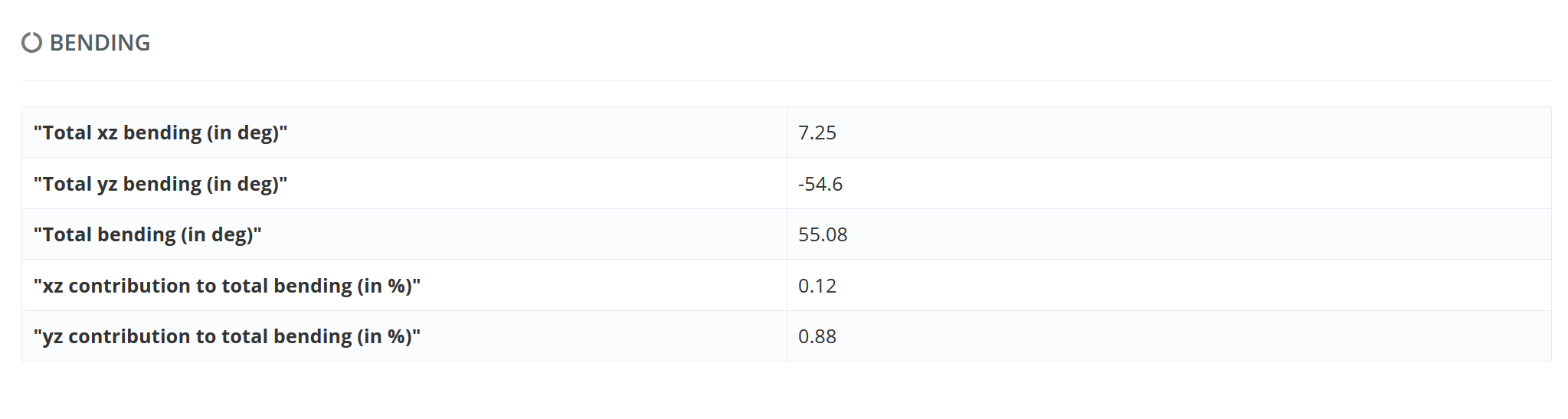
Legend
Total xz bending (in deg): `b_1^x(N)`
Total yz bending (in deg): `b_1^y(N)`
Total bending (in deg): `B_1^{t ot}(N)`
xz contribution to total bending (in %): $b_1^x(N) \over B_1^{t ot}(N)$
yz contribution to total bending (in %): $b_1^y(N) \over B_1^{t ot}(N)$
Bending distribution of 5/10 bp segments (available for Structure Flexibility Analysis)
The plot contains the distribution of all possible 5/10bp segments of the DNA fiber of the relaxed structure. The probability distribution is normalized such as that the area of the probability distribution is one. The x-axis shows the bending in degree, the y axis marks the probability.
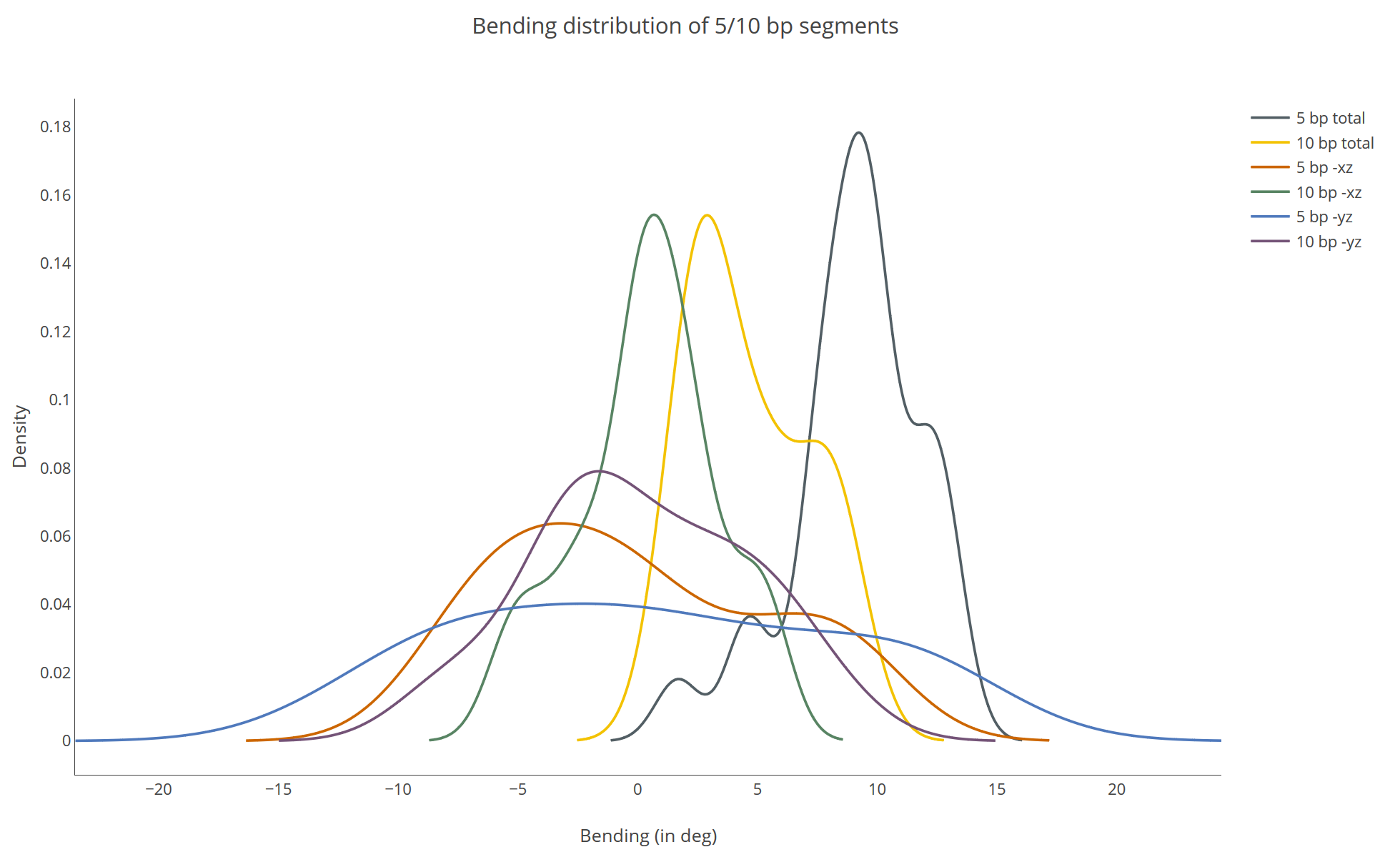
Explanation of the legend
5bp total: Distribution of all `B_n^{t ot}(5)`
10bp total: Distribution of all `B_n^{t ot}(10)`
5 bp –xz: Distribution of all `b_n^x(5)`
10 bp –xz: Distribution of all `b_n^x(10)`
5 bp –yz: Distribution of all `b_n^y(5)`
10 bp –yz: Distribution of all `b_n^y(10)`
Bending distribution of 5/10 bp segments and the whole fiber (available for Trajectory Flexibility Analysis)
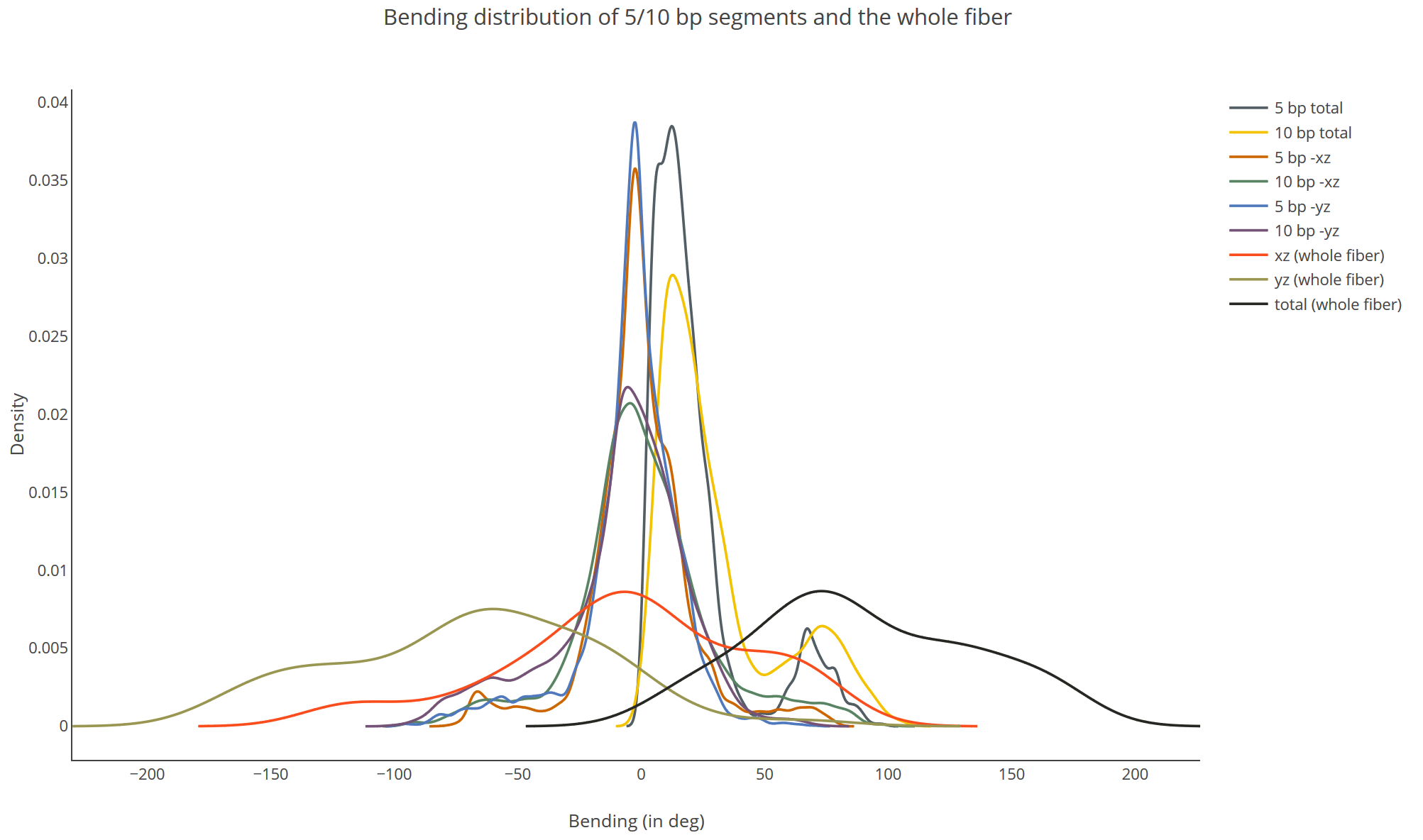
The plot contains the probability distribution of all possible 5/10bp segments of the DNA fiber of all snapshots in the trajectory. The probability distribution is normalized such as that the area of the probability distribution is one. The x-axis shows the bending in degree, the y axis marks the probability.
Explanation of the legend
5bp total: Distribution of all `B_n^{t ot}(5)`
10bp total: Distribution of all `B_n^{t ot}(10)`
5 bp –xz: Distribution of all `b_n^x(5)`
10 bp –xz: Distribution of all `b_n^x(10)`
5 bp –yz: Distribution of all `b_n^y(5)`
10 bp –yz: Distribution of all `b_n^y(10)`
xz (whole fiber): Distribution of all `b_1^x(N)`
yz (whole fiber): Distribution of all `b_1^y(N)`
total (whole fiber): Distribution of all `B_1^{t ot}(N)`
while N is the total length of the DNA fiber in base-pairs.
Bending of 5/10 bp segments in xz/yz direction along sequence
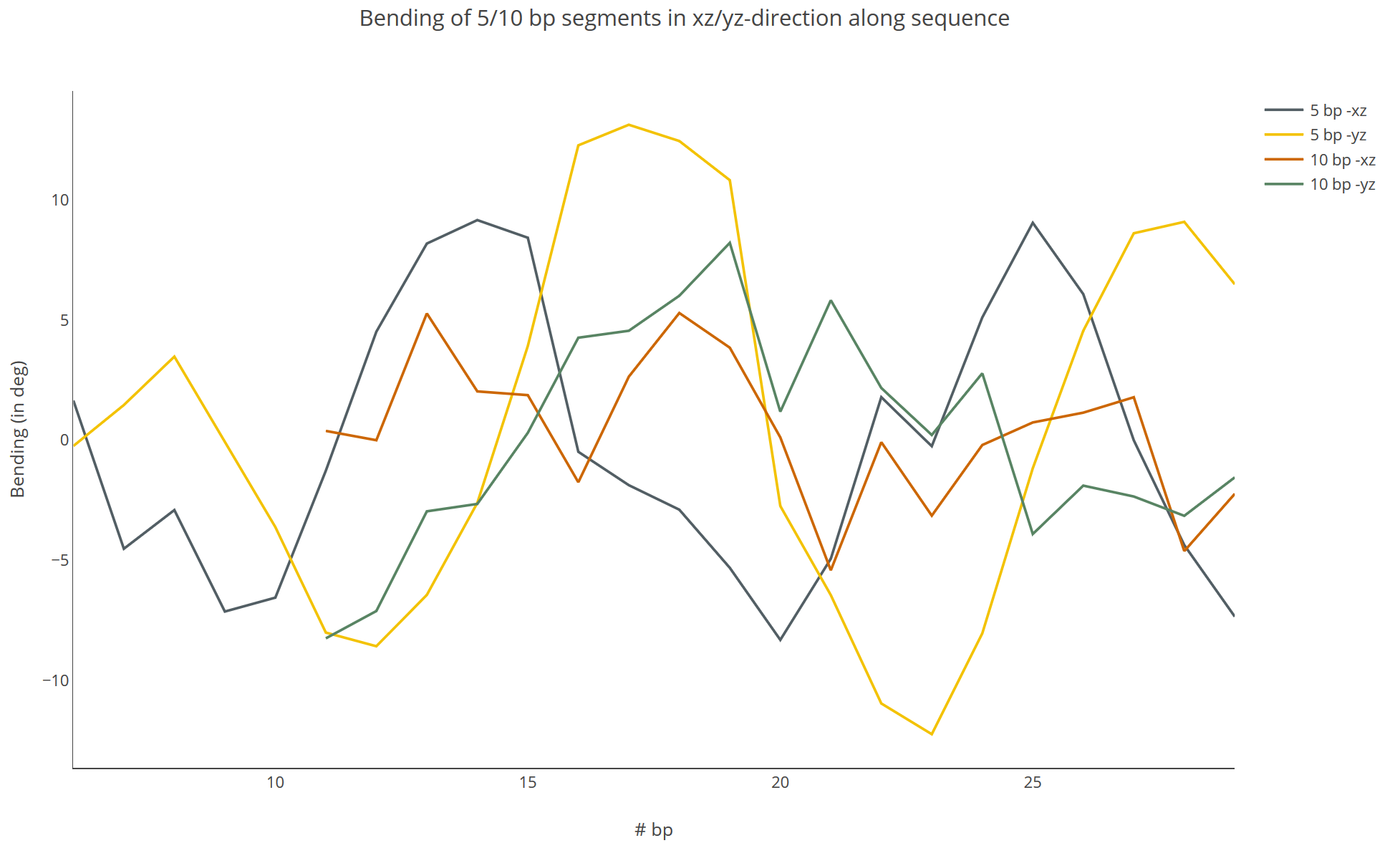
Values of bending (in degree) of the fiber. The x-axis represents all possible values of k+n-1 (the last base pair of the evaluated segment; see formulas above), the y-axis shows the bending value in degree. “Structure Flexibility Analysis” shows the values from the relaxed structure. In the case of “Trajectory Flexibility Analysis” the value displayed is the average over all snapshots.
Legend
5 bp –xz: `b^x(5)`
10 bp –xz: `b^x(10)`
5 bp –yz: `b^y(5)`
10 bp –yz: `b^y(10)`
Distribution of contributions of xz- and yz-bending to total bending of whole fiber (available for Trajectory Flexibility Analysis)
This plot shows the values of $b_1^x(N) \over B_1^{t ot}(N)$ and $b_1^y(N) \over B_1^{t ot}(N)$ of each snapshot of the trajectory as a probability distribution. The probability distribution is normalized such as that the area of the probability distribution is one. The x-axis shows the contribution in % and the y-axis shows the probability.
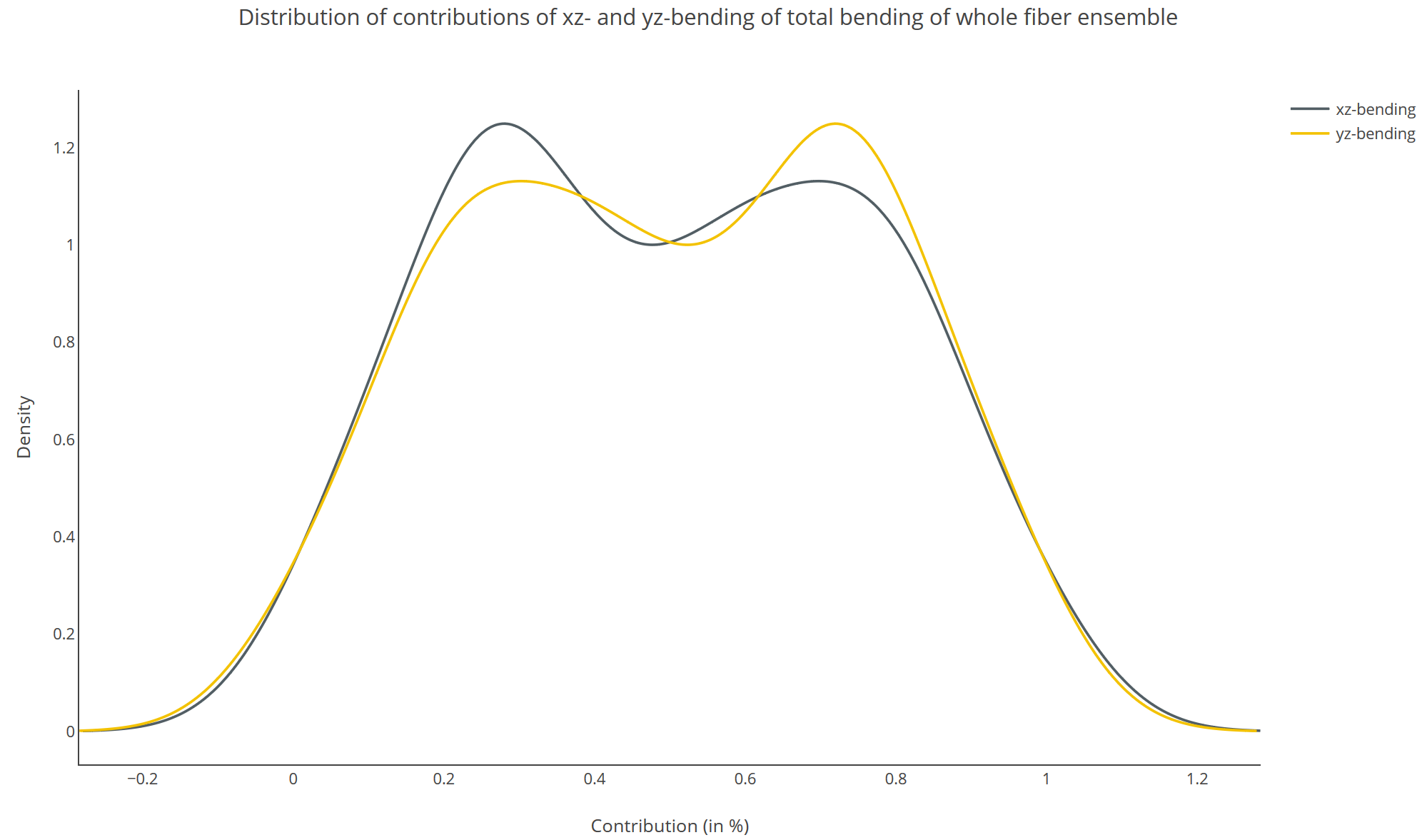
Legend
xz-bending: Distribution of all $b_1^x(N) \over B_1^{t ot}(N)$
yz-bending: Distribution of all $b_1^y(N) \over B_1^{t ot}(N)$
Bending of whole fiber along trajectory (available for Trajectory Flexibility Analysis)
This plot shows contributions of xz- and yz-bending to the total bending of the fiber as well as the absolute values of xz-, yz- and total bending for each snapshot of the trajectory. The x-axis shows the number of snapshots. There are two different y-axes in this interactive plot. The left y-axis marks the values contribution of xz- and yz-bending to the total bending in %. This axis is only valid for the graphs with a ‘%’ sign in the legend. The right y-axis shows the bending in degree and is only valid for the graphs which say ‘(deg)’ in the legend. Both types of graphs can be shown in the same plot window.

Legend
xz-bending (%): $b_1^x(N) \over B_1^{t ot}(N)$
yz-bending (%): $b_1^y(N) \over B_1^{t ot}(N)$
xz bending (deg): `b_1^x(N)`
yz bending (deg): `b_1^y(N)`
total bending (in deg): `B_1^{t ot}(N)`
