MC DNA Help - Method
Method Help
In MC DNA, DNA is represented intrinsically at base pair step level. Rigid base-pairs are connected via elastic potentials modulating the interactions of neighboring base-pairs in a given tetramer environment. The six interactions are given by six base-pair step coordinates: three translational (shift, slide, rise) and three rotational (tilt, roll, twist) degrees of freedom.

The parameters of the elastic potentials (stiffness constants and ground state) for each base-pair step with its nearest neighbors are derived (formulas see Lankas et al., BJ, 2003 or in the help “Analysis -> Stiffness”) from the miniabc set (the smallest set of sequences (13 sequences à 18 bp) in which all 136 unique tetramers appear) of atomistic molecular dynamics simulations simulated with the parmbsc1 force field (Ivani et al., Nature Methods, 2015).
MC DNA
MC DNA runs a Metropolis Monte Carlo algorithm on the six base-pair step parameters with the elastic energy as objective function. After convergence, the bp-step parameters of the final configuration is transformed into a three-dimensional atomistic/coarse grain representation (see 'Inputs') of the DNA molecule. The Cartesian reconstruction based on the six base-pair step coordinates uses rotational matrices and a mid-step frame as ruled out in Lu et al., JMB, 1997. The atomistic positions of the base pairs are reconstructed based on the position and orientation of the center of the base pair.
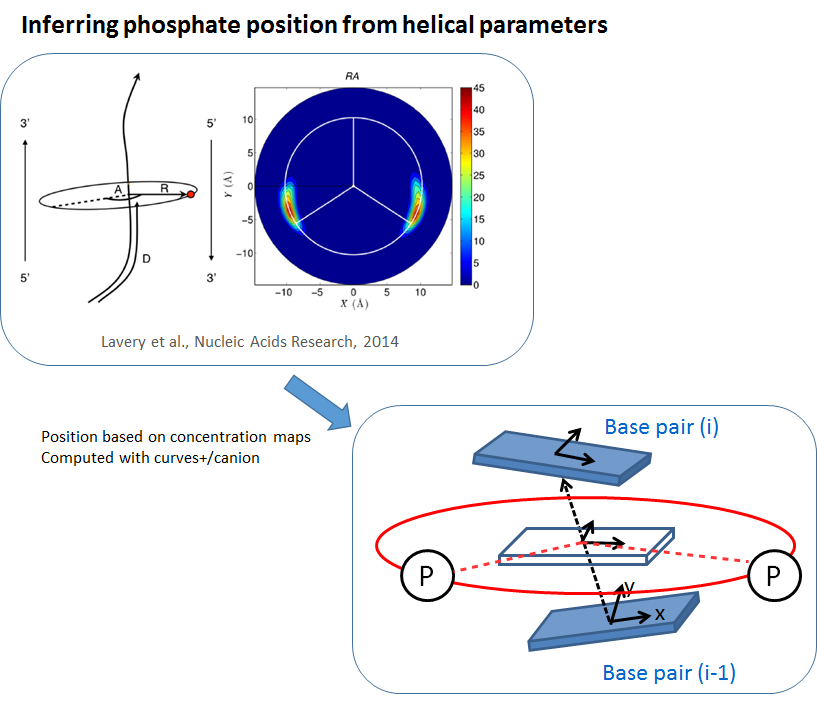
The phosphates of the backbone are added based on results by Lavery et al. (2014) where it was found that the phosphates are positioned at a certain distance and a certain angle relative to the helical axis (Figure top left). We define the helical axis between two base pairs i-1 and i as the connection of its two centers and the orientation as the average orientation of the two base-pairs i-1 and i. The position of the phosphates can then be inferred as shown on the bottom right part of the figure. The resulting structure with the base pairs in atomistic resolution and the phosphates of the backbone is called “Coarse Grain” resolution. To reach “Atomistic” resolution the backbone of the DNA is reconstructed with the AMBER software. The positions of the phosphate and of the atoms of the base pairs stay fixed in this reconstruction process.
Circular MC DNA
The algorithm for circular MC DNA is performing local Monte Carlo moves to maintain the overall structure (for theoretical background about circular DNA check the last paragraph of this secion). We call this procedure 'segmental Monte Carlo' algorithm. In the simulation of circular MC DNA the starting structure is a plane circle with the total twist according the change in the linking number $\Delta Lk$. To construct the circular starting structure two steps are needed. First the linear starting structure was constructued with NAB by AmberTools. In the second step the planar circles are built with a program designed by Charles Laughton which is described in Harris et al., NAR (2008). In the following the 'segmental Monte Carlo' move is explained. In a usual Monte Carlo move for unconstrained DNA internal coordinates of a bp step are changed which induces a rigid body move of the DNA above the changed bp step.
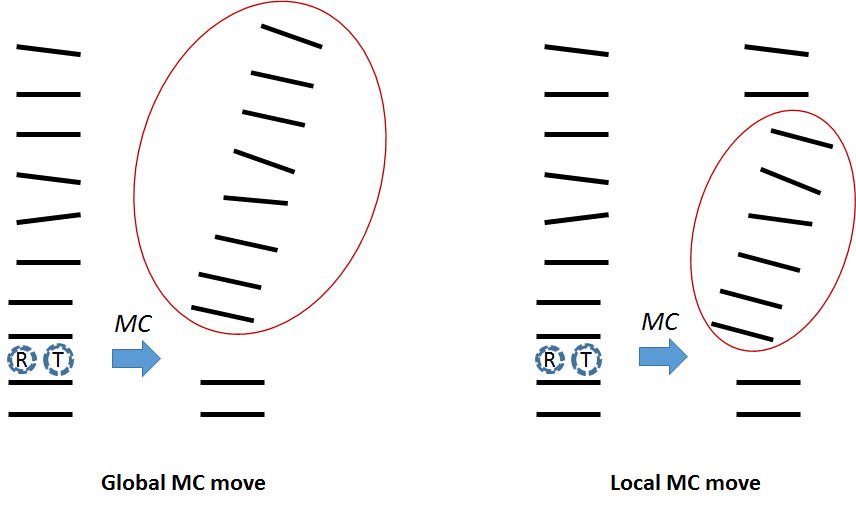
In the constrained circular model we change the coordinates of bp-step i, however the rigid body move is done only for a segment of DNA of n base-pairs in length above the changed bp step (see Figure above). The procedure of the segmental Monte Carlo move with a segment length of n is explained in the Figure below. The orientation of bp i+2 until i+n is kept unchanged compensated by a change in rotational parameters of step i+1 (see 'Orient' in the figure below). A recursive stochastic closure algorithm (RSC) adapted from Minary and Levitt (JCB, 2010) is applied to fix the position of the base pair i+n to its original position and to adapt positions of the n-1 base pairs within this segment. The parameter n is set to 5 to obtain optimal results. This “segmental” Monte Carlo move assures that the circle is always in a closed form throughout the simulation. After every successful Monte Carlo move the circle is examined for steric clashes. If steric clashes are detected the Monte Carlo move gets rejected. This procedure is very important for circles with high $\Delta Lk$ since circles with high superimposed stress tend to physically contact in their supercoiled state.

Theoretical background of circular DNA: An important feature of a circle is that the linking number $\Delta Lk = Tw + Wr$ is constant. Twist Tw reflects the number of helical turns and writhe Wr is the number of times the double helix crosses over on itself (supercoils). The relaxed structure for the circle is defined as the structure with Wr = 0 and twist values are the values of the relaxed twist state. Thus the total linking number $Lk_0$ of the relaxed circle is $Lk_0 = Tw_0$. To induce additional stress the twist value of each base pair step of the circle can be changed which results in new value of Tw. Over- or under-twisting of the relaxed structure results in a different linking number $\Delta Lk = Lk - Lk_0 = Tw - Tw_0$ and thus a different starting structure with $\Delta Lk \ne 0$. $\Delta Lk$ can only take integer numbers. $\Delta Lk = Tw + Wr$ will stay constant throughout the whole simulation, however Tw will change throughout the simulation and Wr becomes non-zero. The value of $\Delta Lk$ can be chosen in the Input parameters and the values of Tw and Wr of the final structure of the simulation can be viewed in the “Circular” analysis.
MC DNA + Proteins
The algorithm of “MC DNA + Proteins” works the same way as the unconstrained MC DNA with Monte Carlo moves on the six base-pair step parameters with the elastic energy as objective function. However the DNA which is bound to the protein is constrained. The base-pairs bound to the protein are kept rigid with the six base-pair step parameters extracted with CURVES from the X-ray crystal structure of the protein-DNA complex in the PDB. In the “Input” section you can choose the protein of interest from an extensive list of protein-DNA complexes. For example the protein-DNA complex 1a0a is bound to 16 base pairs of DNA. If you choose in the 'Input' initial position 2, the base pair steps 2 to 17 (base pair 3 to 18) are kept rigid according to the base pair step parameters of the DNA in the 1a0a complex. The sequence the user inputs for the bound DNA does not matter in this case.
Note: The protein itself does not directly contribute to the simulation (apart from the conformation imposed on the protein-bound DNA), however in the 3D output of the structure/trajectory the protein structure of the protein-DNA complex is superimposed onto the DNA for visualization and analysis purposes.
